この記事は、中小企業診断士一次試験におけるファイナンス分野の攻略記事です。概要については、こちらをご覧ください。
今日のテーマは、リターンとリスクです。初めにこの範囲の平成27~30年の出題を確認します。
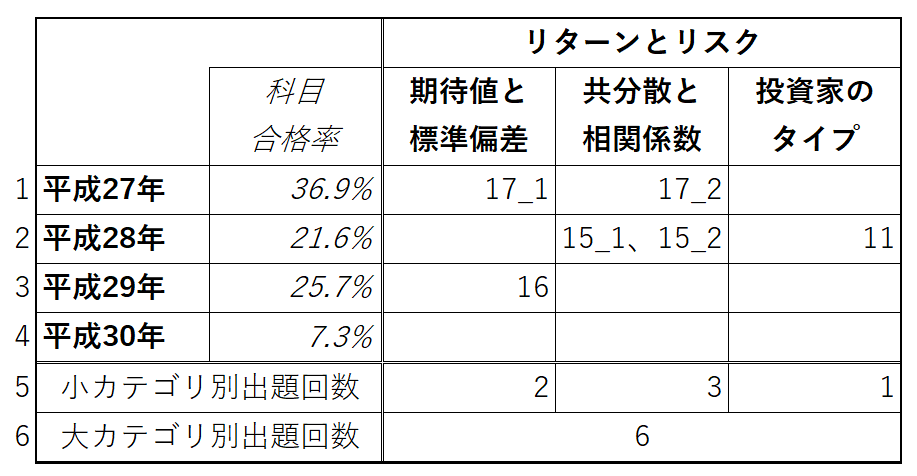
割とまんべんなく出題されていますね。中でも、共分散と相関係数の問題は、「一般には」難度が高いと言われていますので、重点的に取り扱います。
期待値と標準偏差、共分散と相関係数
さて、早速問題を解いていきましょう。なお、設問文はすべて多少表現を短くしていますが(一応著作権が気になったので…)、選択肢はそのまま使用させて頂きました。
平成27年 第17問
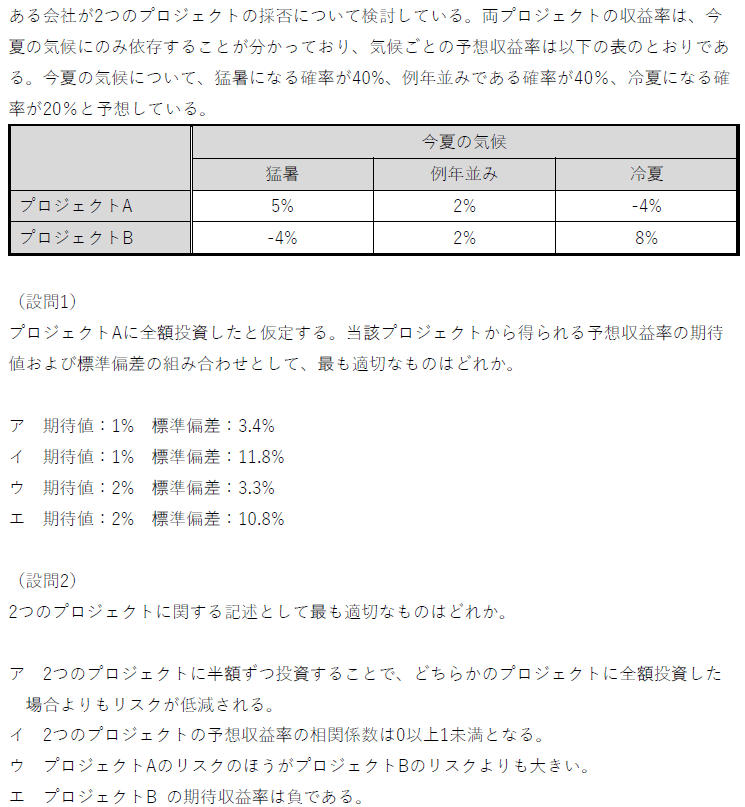
フレームワークのご紹介
この手のタイプの問題はこちらの手順に正しく従えば、まず間違いなく解けます(但し、手計算はかなりだるいです…)。
- (それぞれの資産orプロジェクトの)期待リターンを求める
- (それぞれの資産orプロジェクトの)1.で求めた期待リターンを使って、分散を求める
- (それぞれの資産orプロジェクトの)分散の平方根をとって標準偏差を求める
- 1.で求めたそれぞれの期待リターンを使って、共分散を求める
- 4.で求めた共分散/3で求めた標準偏差の積、で相関係数を求める
模範受験生解答(フレームワークの利用)

(設問1)上記より、期待値:2%、標準偏差:3.3%となり、ウ
(設問2)上記より、
イ 2つのプロジェクトの予想収益率の相関係数は0以上1未満となる。
→誤り:相関係数<0
ウ プロジェクトAのリスクのほうがプロジェクトBのリスクよりも大きい。
→誤り:Aの標準偏差:3.29%<Bの標準偏差:4.49%
エ プロジェクトB の期待収益率は負である。
→誤り:Bの期待値:0.8%
となり、消去法でア
正解の選択肢にたどり着けたわけですが、これをプレッシャーのかかる試験中にやりますか?計算ミスして一度焦りだすと、めちゃめちゃ時間かかりそう…(電卓使えないっすよ?w)そこで以下の方法を提案します!
ダンナ的解答(計算は極力しない!)
ポイントは、標準偏差や共分散・相関係数の手計算はめんどくさいので、それらしい答えを選んでおき、時間が余ったら、計算する、ということです。先に、ダンナ流解答をご紹介します。
(設問1)選択肢を見た瞬間に、アとウに絞る(下の「標準偏差に関する常識」を参照ください)。 期待リターンだけはちゃんと計算して、答はウ
(設問2)選択肢を見た瞬間に、アが答(下の「相関係数に関する常識」を参照ください)。 一応、他の選択肢も見ると、イは、2つのプロジェクトは負の相関(一方が増えると他方は減る関係)だから明らかに違う(下の「相関係数に関する常識」を参照ください)。期待リターンを計算すると、エもすぐに落とせる。とりあえず、アにマークしておいて、時間が余ったら、標準偏差を計算してウを検証する。
と、こんな感じで、2問合わせて1分かけずにさばきます。時間がかからないのは当然です。期待リターン以外計算しないのですからwでも、なぜ計算しなくてもある程度絞れるのでしょうか?みなさんがおそらく首をかしげたであろう、解答内にハイライトした箇所について、順番に説明します。
標準偏差に関する常識
- 標準偏差は、確率分布が期待値(平均)周りにどれだけ広がっているかを表している(と考える)
- 具体的には、(確率分布が正規分布のときは)期待値から1標準偏差以内に全体の68%は収まる
- したがって、期待値と標準偏差の大きさはそれほど変わらない(10倍以上違うのは不自然)
下のようなグラフをどこかで見たことがあると思います。本問は、正規分布を前提とした問題ではありません。しかし、診断士試験で出題される問題が極端にヘンテコな確率分布に従うような問題であることは考えづらいので、これらの知識は正確ではないものの相応に役立つだろうと思います。
本問の場合だと、期待リターンが2%なので、例えば、標準偏差が10%だとすると、-8%(=2%-10%)から12%(=2%+10%)の中に全体の68%が収まることになります。これは、設問(最大でも5%、最小でも-4%)と比べて、あまりに分布の広がりが大きすぎます。一方、標準偏差が3%だとすると、-1%(=2%-3%)から5%(=2%+3%)の中に全体の68%が収まることになります。こちらの方が明らかに自然ですよね。

完全にご参考ですが、私たちが学生の頃からなじみのある「偏差値」も上の正規分布のグラフで簡単に理解できます。要するに、平均点=偏差値50、1標準偏差=10としたものが偏差値なので、(得点分布が正規分布の場合)偏差値40~60の学生を集めると全体の68%を占めていることになりますね。言い換えれば、偏差値60の学生は、全体の半分よりも34%(=68%/2)上位にいるはずなので、上位16%の学生といえます。同様に、偏差値70の学生は、全体の半分よりも47.5%(=95%/2)上位にいるはずなので、上位2.5%の学生といえます。
試験対策上は、期待値と標準偏差の大きさはそれほど変わらない(10倍以上違うのは不自然)とだけ覚えればいいと思いますが、自分なりに理解して頂ければ幸いです。あと、ある選択肢の標準偏差を2乗すると、他の選択肢の標準偏差に近そうな場合、大抵小さい方の値が答えとなります(要は、分散とひっかけて作問しているわけですねw)。本問だと、確かに、3.3×3.3=10.89、になってます。
相関係数に関する常識
あえてふわっと(=厳密性を無視して)書いていますが、下の表だけ頭に叩き込んでください。問題を解くだけなら、これで十分です。付言すると、\(\rho = 1\)の場合って滅多にないので、分散投資をすると、大抵リスクは減ります。なお、表の一番下の「リスク・リターン平面におけるポートフォリオの形状」については、次回扱います。
| 相関係数\(\rho \) | \(\rho = -1\) | \(-1<\rho < -0.3\) | \(-0.3 \leq \rho \leq 0.3\) | \(0.3<\rho < 1\) | \(\rho = 1\) |
| 相関の大きさ | 完全な負相関 | 負の相関 (一方が増えると他方は減る) | 2変数の相関は弱い | 正の相関 (一方が増えると他方も増える) | 完全な正相関 |
| 分散効果 | 最大 | 大きい | 存在 | 小さいが存在 | ゼロ |
| リスク・リターン平面におけるポートフォリオの形状 | 折れ線 (リスクが0になる点で折れる) | 開きがきつい放物線 | 開きがややきつい放物線 | 開きがゆるい放物線 | 直線 |
これにて、一通り必要な道具については、(一つを除いて)ひと通り説明したのでもう1問類題を解いてみましょう。
平成28年 第15問
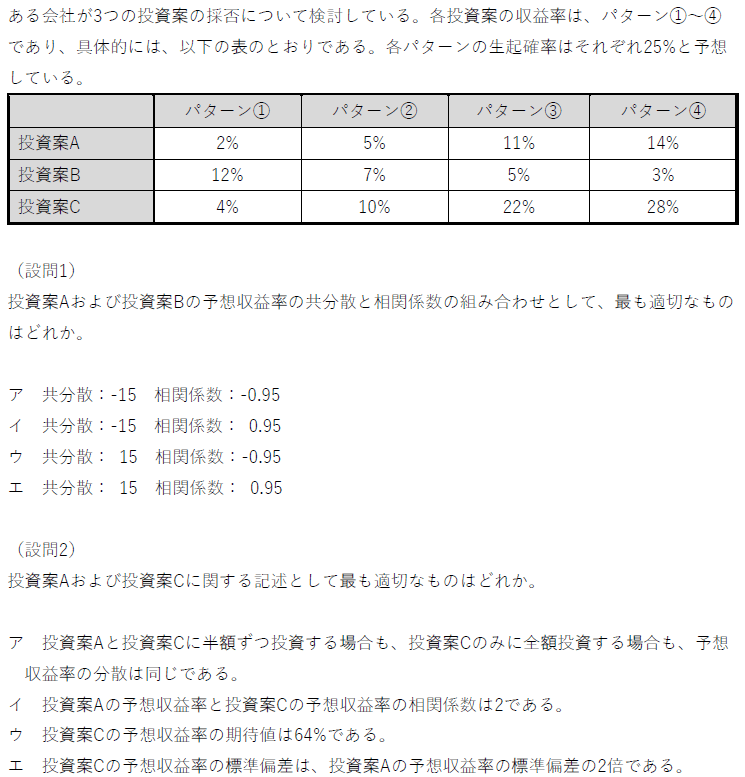
本問も極力計算しない方針で回答しますw
(設問1)選択肢を見た瞬間に、アとエに絞る(共分散と相関係数の符号は、絶対に同一になる)。 パターン①→④とみていくと、投資案Aが増加するのに対して、投資案Cは減少していることがわかる。すなわち、両者は逆相関。よって、答はア
(設問2)選択肢を見た瞬間に、イは落とす(相関係数は-1から1の間の値)。ウをみて、明らかにリターンの水準が高すぎるのに気づく。設問にあるリターンの表と比べても、やはりあり得ないので落とす。ここまで順調だが、アとエは計算しないとわかんない…?
これまでお読みいただいた方は、きっと上のような状況になっていると思います。アとエのどちらを選ぶかについては、分散と標準偏差を正しく計算すればいいのですが、以下の知識があれば、計算はほぼなくて回答できます。
期待値\(E(X)\)・分散\(V(X)\)に関する常識
- 期待値について、\(aE(X)=E(aX)\)が成り立つ。つまり、確率変数\(X\)が\(a\)倍になると、期待値も\(a\)倍になる。
- 分散について、\(a^2V(X)=V(aX)\)が成り立つ。つまり、確率変数\(X\)が\(a\)倍になると、分散は\(a^2\)倍になる。
早速使ってみましょう。
設問をよくみると、投資案Aの収益率を2倍すると、投資案Cの収益率になっています。ということは、先ほどの二つ目の知識より、投資案Cの収益率の分散は投資案Aの収益率の分散の4倍となっているはずです。分散の平方根が標準偏差だったので、投資案Cの収益率の標準偏差は投資案Aの収益率の標準偏差の2倍であることがわかります。つまり、エが正解となります。
折角なので、アもみておきましょう。投資案Aの収益率を\(X\)とすると、投資案Aと投資案Cに半額ずつ投資する場合の収益率は、\(0.5×X+0.5×2X=1.5X\)となります。投資案Cのみに全額投資する場合の収益率は、\(2X\)となります。すなわち、前者の場合の収益率の分散は、投資案Aの収益率の分散の\(1.5^2=2.25\)倍、後者の場合の収益率の分散は、投資案Aの収益率の分散の\(2^2=4\)倍となるので、選択肢アは間違っていることがわかります。
最後は少し難しかったですが、最低限の知識さえあれば、計算を最小化して、時間をかけずに解答できることがわかりました(^^)/疲れたあなたには、箸休めのこの一問をプレゼントしますw
平成29年 第16問

簡単なので、解説は省略します。答えはエですw
この程度の問題も出題されているようですね。
投資家のタイプ
ここは下の図を覚えて頂ければ終了です。覚えていなければ、それはそれで終了ですw
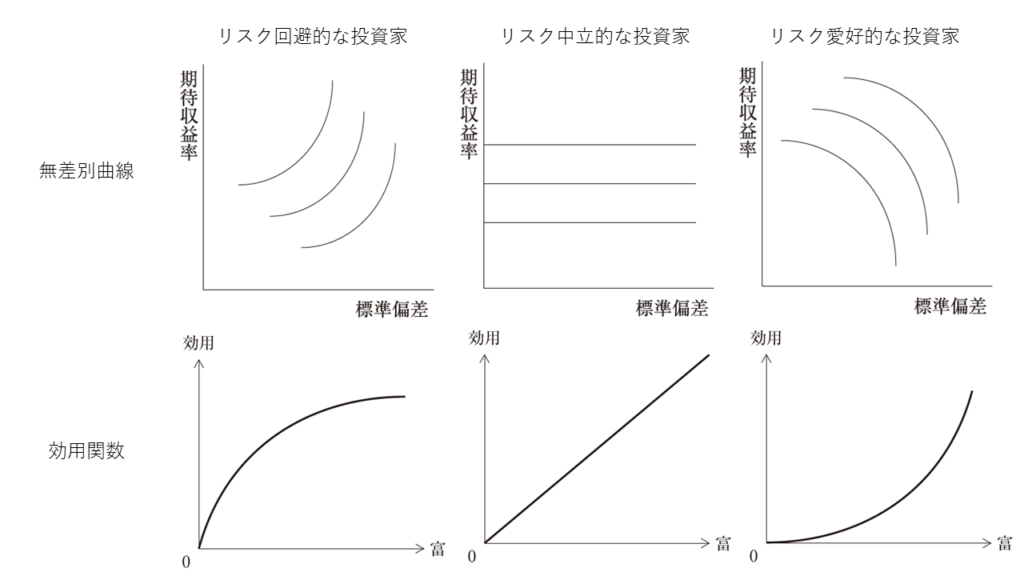
覚え方としては、まずリスク中立的な投資家は直線だと覚えましょう。次に、リスク回避的投資家は、普通の人なんだという意識をもって、グラフを眺めます。無差別曲線の図については、普通の人はリスクが大きくなればなるほど、リターンを大きく要求するはずなので左上のようになります。効用関数については、富が大きくなればなるほど、幸福度合いはそれほど増えていかないことから、左下のようになります。どんなに好きなものでも、多すぎると飽きますよね?だって、普通の人ですからw
このほか、今回の解法が役立つ近年の出題
平成28年第11問でリスク中立的な投資家とリスク回避的な投資家についての効用関数のグラフを選ばせる問題が出題されています。また、平成25年第19問でリスク回避的な投資家の無差別曲線のグラフを選ばせる問題が出題されています。
財務・会計 ファイナンス徹底攻略 その2まとめ
- 「期待値と標準偏差、共分散と相関係数」に関する問題は、最小限の知識があれば、ほとんど計算せずに解答可能
- 特に、標準偏差や相関係数については、常識が大いにものをいう世界
- 「投資家のタイプ」に関する問題は、グラフを6枚頭に入れることができればOK
- 今後も、本ブログでは、重要論点の絞り込みや(世の中に出回っていない)早く解ける裏技を執筆予定
次回は、いよいよ「ポートフォリオ理論」を扱います。
これからもどうぞよろしくお願いします!




